The purpose of this problem is to set the stage for some major
applications of Calculus that we will discuss later this semester.
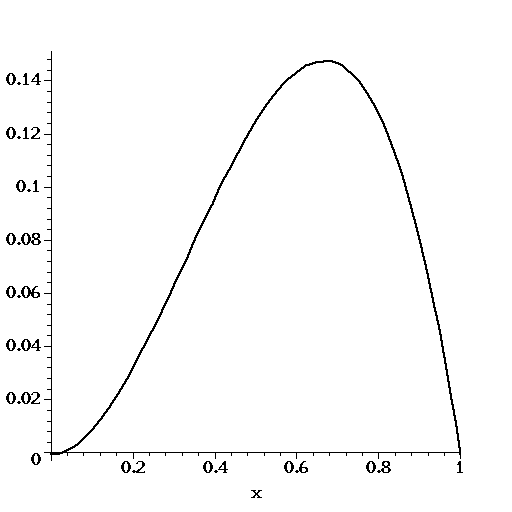
The Figure above shows the graph of on the
interval . Clearly the function value assumes a maximum of about
0.15 at a value of that's close to 0.7.
Within a month or so it will be a very simple matter indeed to
figure out the precise maximum value of and the value of
where that maximum occurs.
If you have taken Calculus before you may already know how to do this,
or a tutor can show you how to do this without even breathing hard.
However, to get the most benefit from this problem, determine the
maximum value of and the corresponding value of
numerically without the use of Calculus. Use your calculator to
evaluate at many points, or use its graphing facility to zoom in
on the maximum. You will appreciate the power of your new skills when
you revisit this problem later this semester and solve it using the tools of
Calculus. WeBWorK will accept your answer below if it is within one
tenth of one percent of the true answer.
assumes it maximum value of
at
.
You can earn partial credit on this problem.