The blood vascular system consists of blood vessels (arteries,
arterioles, capillaries, and veins) that convey blood from the
heart to the organs and back to the heart. This system should
work so as to minimize the energy expended by the heart in
pumping the blood. In particular, this energy is reduced when
the resistance of the blood is lowered. One of Poiseuille's
Laws gives the resistance of the blood as
where is the length of the blood vessel, is the radius,
and is a positive constant determined by the viscosity of
the blood. The figure shows a
main blood vessel with radius branching at an angle
into a smaller vessel with radius . (Note in your
answers use instead of and and respectively
instead of and .)
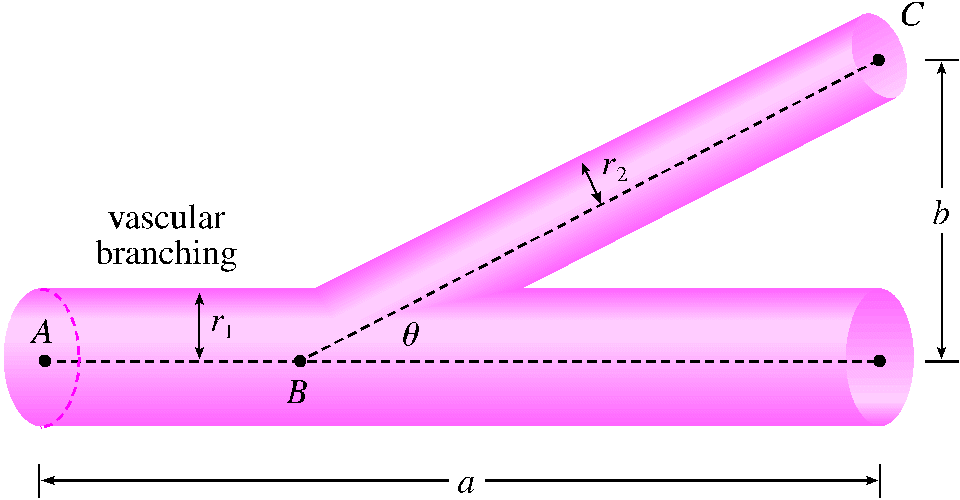
(a) Use Poiseuille's Law to find the total resistance of the
blood along the path where and are the distances shown
in the figure. (Your answer may depend on , , , , ,
and .)
=
(b) Find the value of which minimizes the
resistance. (Your answer may depend on , , , , and .)
=
(c) Find the optimal branching angle when the radius of the
smaller blood vessel is the radius of the larger vessel.
=

You can earn partial credit on this problem.